题目:有 n 个人前来排队买票,其中第 0 人站在队伍 最前方 ,第 (n - 1) 人站在队伍 最后方 。
给你一个下标从 0 开始的整数数组 tickets ,数组长度为 n ,其中第 i 人想要购买的票数为 tickets[i] 。
每个人买票都需要用掉 恰好 1 秒 。一个人 一次只能买一张票 ,如果需要购买更多票,他必须走到 队尾 重新排队(瞬间 发生,不计时间)。如果一个人没有剩下需要买的票,那他将会 离开 队伍。
返回位于位置 k(下标从 0 开始)的人完成买票需要的时间(以秒为单位)。
提示:
n == tickets.length
1 <= n <= 100
1 <= tickets[i] <= 100
0 <= k < n
思路:排在k前的人:
如果想购买的票数大于tickets[k],在k买完前会买tickets[k]张票;
如果想购买的票数小于等于tickets[k],在k买完前会买tickets[i]张票;
k买tickets[k]张票
k之后的人 :
如果想购买的票数大于等于tickets[k],在k买完前会买tickets[k]-1张票;
如果想购买的票数小于tickets[k],在k买完前会买tickets[i]张票;
时间复杂度O(n)
空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int timeRequiredToBuy(int[] tickets, int k) {
int res = 0;
for (int i = 0; i < tickets.length; i++) {
if (tickets[i]>0){
if (i<=k){
res+=Math.min(tickets[i],tickets[k]);
} else {
res+=Math.min(tickets[i],tickets[k]-1);
}
}
}
return res;
}
}
|
给你一个链表的头节点 head 。
链表中的节点 按顺序 划分成若干 非空 组,这些非空组的长度构成一个自然数序列(1, 2, 3, 4, …)。一个组的 长度 就是组中分配到的节点数目。换句话说:
节点 1 分配给第一组
节点 2 和 3 分配给第二组
节点 4、5 和 6 分配给第三组,以此类推
注意,最后一组的长度可能小于或者等于 1 + 倒数第二组的长度 。
反转 每个 偶数 长度组中的节点,并返回修改后链表的头节点 head 。
提示:
链表中节点数目范围是 [1, 105]
0 <= Node.val <= 105
思路:直接模拟,先计算组的长度,再判断是否反转
时间复杂度O(n)
空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public ListNode reverseEvenLengthGroups(ListNode head) {
ListNode res = new ListNode();
res.next = head;
int num = 2;
while (head.next!=null){
int count = 0;
ListNode node = head;
while (node.next!=null&&count<num){
node = node.next;
count++;
}
if (count%2==0){
ListNode last = head;
head = head.next;
while (head.next!=null&&count>1){
ListNode temp = last.next;
last.next = head.next;
head.next = last.next.next;
last.next.next = temp;
count--;
}
}else{
while (head.next!=null&&count>0){
head = head.next;
count--;
}
}
num++;
}
return res.next;
}
}
|
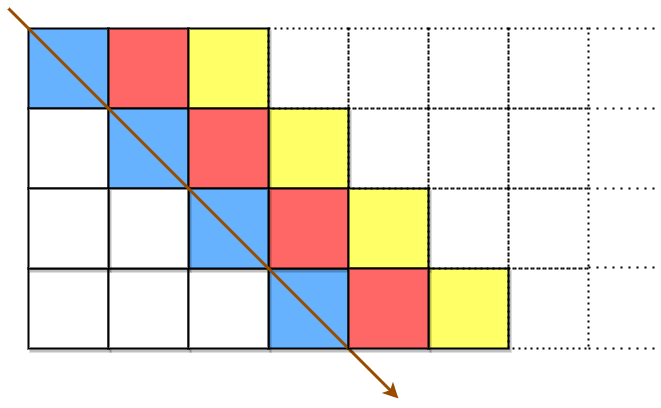
先填充蓝色单元格,接着是红色单元格,然后是黄色单元格,以此类推,直到到达 originalText 末尾。箭头指示顺序即为单元格填充顺序。所有空单元格用 ‘ ‘ 进行填充。矩阵的列数需满足:用 originalText 填充之后,最右侧列 不为空 。
接着按行将字符附加到矩阵中,构造 encodedText 。
先把蓝色单元格中的字符附加到 encodedText 中,接着是红色单元格,最后是黄色单元格。箭头指示单元格访问顺序。
例如,如果 originalText = “cipher” 且 rows = 3 ,那么我们可以按下述方法将其编码:
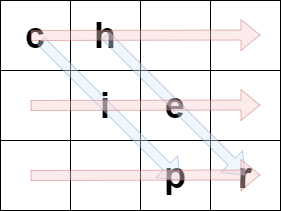
蓝色箭头标识 originalText 是如何放入矩阵中的,红色箭头标识形成 encodedText 的顺序。在上述例子中,encodedText = “ch ie pr” 。
给你编码后的字符串 encodedText 和矩阵的行数 rows ,返回源字符串 originalText 。
注意:originalText 不 含任何尾随空格 ‘ ‘ 。生成的测试用例满足 仅存在一个 可能的 originalText 。
思路:先按行数拆分encodedText ,得到每一行,然后从(0,0…n)开始斜向下遍历,最后去掉末尾空格
时间复杂度O(n)
空间复杂度O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public String decodeCiphertext(String encodedText, int rows) {
String[] row = new String[rows];
int len = encodedText.length()/rows;
for (int i = 0; i <rows; i++) {
row[i] = encodedText.substring(0+i*len,len+i*len);
}
StringBuilder res = new StringBuilder();
for (int i = 0; i < len; i++) {
for (int j = 0; j < rows&&i+j<len; j++) {
res.append(row[j].charAt(i+j));
}
}
for (int i = res.length()-1; i >=0; i--) {
if (res.charAt(i)!=' '){
return res.substring(0,i+1);
}
}
return "";
}
}
|
给你一个整数 n ,表示网络上的用户数目。每个用户按从 0 到 n - 1 进行编号。
给你一个下标从 0 开始的二维整数数组 restrictions ,其中 restrictions[i] = [xi, yi] 意味着用户 xi 和用户 yi 不能 成为 朋友 ,不管是 直接 还是通过其他用户 间接 。
最初,用户里没有人是其他用户的朋友。给你一个下标从 0 开始的二维整数数组 requests 表示好友请求的列表,其中 requests[j] = [uj, vj] 是用户 uj 和用户 vj 之间的一条好友请求。
如果 uj 和 vj 可以成为 朋友 ,那么好友请求将会 成功 。每个好友请求都会按列表中给出的顺序进行处理(即,requests[j] 会在 requests[j + 1] 前)。一旦请求成功,那么对所有未来的好友请求而言, uj 和 vj 将会 成为直接朋友 。
返回一个 布尔数组 result ,其中元素遵循此规则:如果第 j 个好友请求 成功 ,那么 result[j] 就是 true ;否则,为 false 。
注意:如果 uj 和 vj 已经是直接朋友,那么他们之间的请求将仍然 成功 。
提示:
2 <= n <= 1000
0 <= restrictions.length <= 1000
restrictions[i].length == 2
0 <= xi, yi <= n - 1
xi != yi
1 <= requests.length <= 1000
requests[j].length == 2
0 <= uj, vj <= n - 1
uj != vj
思路:使用并查集维护朋友关系,哈希表维护敌人关系,合并并查集时,遍历每一个敌人,将敌人的root加入哈希表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| class Solution {
public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {
UnionFind unionFind = new UnionFind(n);
for (int i = 0; i < restrictions.length; i++) {
unionFind.restrict(restrictions[i][0],restrictions[i][1]);
}
boolean[] res = new boolean[requests.length];
for (int i = 0; i < requests.length; i++) {
res[i] = unionFind.union(requests[i][0],requests[i][1]);
}
return res;
}
private class UnionFind {
private int[] parent;
private HashMap<Integer, HashSet<Integer>> map = new HashMap<>();
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
map.put(i,new HashSet<>());
}
}
public int find(int index) {
if (index == parent[index]) {
return index;
}
int root = find(parent[index]);
parent[index] = root;
return root;
}
public boolean union(int index, int p) {
index = find(index);
p = find(p);
if (!map.get(index).contains(p)&&!map.get(p).contains(index)){
if (map.get(p).size()<map.get(index).size()){
index = index^p;
p = index^p;
index = index^p;
}
parent[index] = p;
int finalP = p;
map.get(index).forEach(i-> {
int num = this.find(i);
map.get(finalP).add(num);
map.get(num).add(finalP);
});
return true;
}
return false;
}
public void restrict(int p1,int p2) {
map.get(p1).add(p2);
map.get(p2).add(p1);
}
}
}
|

